Wednesday, October 31, 2007
Identities BOB
BOB 2
BOB
BOB
BOB
The trigonometric identities unit hasn't been too devastating. I'm grasping the concept of proving little by little. Although I do have an issue with all the corrolories and remembering that everything can be written as something else, but I'm working on that.
My issue is with the number one and how it can be written in many endless ways. Going through with proving identies, I always forget that the identity can be written in a different way or I can change it to make it look another way.
I understand sum and difference identies, but I always have to watch out for the "signs" because it will just lead me in the wrong direction, but I'm working my issues out slowly.
I do understand what is going on, but the problem lies with having to apply everything to the questions. Like Mr. K said, there are so many different ways that students can solve the identities. We'll see how the test goes and I hope I don't do too badly.
Good luck everyone.
(I wonder when we get to see our previous tests?)
BOB
BOB
Halloween Scribe Post - New Unit: Exponents
I started off with changing the sin^2x into 1-cos^2x, then multiply it by 2. The moved everything onto the left side, getting 2cos^2x - cosx = 0. Then factor cosx out of it which you'll then get cosx(2cosx -1) = 0. From there you can tell that cosx = 0 and cosx = 1/2 which means x = pi/2, 3pi/2 and x = pi/3 and 5pi/3.
We were then introduced to the new unit; only a very light introduction. We were asked to express the numbers 2, 3, 4/9, and 1/4 in the the forms of exponents. For example, 2 can be express as 4^(1/2), 3 can be expressed as 6561^(1/8), 4/9 can be expressed as (16/81)^(1/2) and 1/4 can be expressed as 2^(-2). You can also give numbers negative exponents, which you would then have to turn the base of the number into it's reciprocal. For example; 4^(1/2) can also be expressed as (1/4)^(-1/2). Notice the base of the number that was previously 4, became 1/4 and the exponent of 1/2 became -1/2. We were then asked to express 1/4 in 10 other ways for tomorrow's class.
Afterwards, we got a little deeper into the subject; now having to find the exponents in the given equation 2^x = 64. That one was a no brainer. But then there was 27^(2x-1) = 3. The way you solve that is to rewrite the equation with both sides of the equal sign having the same base number; for example 27 = 3^3, then you have the base number of 3 on both sides. So (3^3)^(2x-1) = 3^1. You then take the exponents alone, (3)(2x-1) = 1 **note that the "3" in that is the exponent not the base, and the "1" is from the right side of the equation because 3 is the same thing as 3^1**. Then you simply solve for "x";;
3(2x-1) = 1
6x - 3 = 1
6x = 4
x = 4/6 or 2/3
So there you have solved for "x" in the equation 27^(2x-1) = 3
We were also given in the set, 3^x = 1/27. Remembering that negative exponents give you recipricols, the answer must be (-3).
Lastly, we were given this set to solve for x:
4^(1-x) = 8 49^(x-2) = 7 √7 25^2x = 5^(x+6)
the answers are as follows:
4^(1-x) = 8 (2^2)^(1-x) = 2^3
(2)(1-x) = 3
2 - 2x = 3
2x = -1
x = =1/2
49^(x-2) = 7 √7
(7^2)^(x-2) = (7^1)(7^(1/2))
(7^2)^(x-2) = 7^(3/2)
(2)(x-2) = (3/2)
2x - 4 = 3/2
2x = 4 + 3/2
x = 11/4
25^2x = 5^(x+6)
(5^2)^(2x) = 5^(x+6)
(2)(2x) = x+6
3x = 6
x = 2
And that was everything that we covered in Halloween's class, that I'm surprised everyone showed up to. Tomorrow's scribe can be Sergio, he can cover All Saints Day's class for everyone.
Meeelar's Flickr Assignment
Tuesday, October 30, 2007
B0Bb`n itttt again!
Flickr Assignment

The pre-test contain eight questions..
1) Simplify: sin(2x+π)
A. sin2x
B. cos2x
C. -sin2x
D. -cos2x
The answer is C because sin(2x+π) is similar to sin(α+β) and the equation for this is simple, just do the sine dance!
sin(α+β)=sinαcosβ+cosαsinβ .. now you just plug sin(2x+π) into the equation
sin(2x+π)=sin2xcosπ+cos2xsinπ
sin(2x+π)=sin2x(-1)+cos2x(0)
sin(2x+π)=-sin2x+0
sin(2x+π)=-sin2x
cos π= -1
sinπ= 0 anything multiplied by 0 equals 0 so the right side reduces..
2) The terminal arm of an angle Ө in standard position passes through point (m,n) where m>0, n>0. Determine the value of sin(π+Ө).
A. ( -n)/√(m^2+n^2)
B. ( -m)/√(m^2+n^2)
C. ( n)/√(m^2+n^2)
D. ( m)/√(m^2+n^2)
The answer is A.
The question says that m and n are both positive so you know the coordinates are in the first quadrant.
m=x coordinates
n=y coordinates
Ө= angle
Once you draw a diagram you can use the pythagorean theorem to find the hypotunse, which is √(m^2+n^2).
Since sin=Opposite/adjacent then..
n/√(m^2+n^2)
BUT... it asks for the value of sin(π+Ө) so you substitute it in the sin(α+β)=sinαcosβ+cosαsinβ when you finish you get -sinӨ. Soo.. you multiply everything by -1.
And your answer is
-n/√(m^2+n^2).
Question# 3.

In this slide mr.k drew a diagram of cos A and you realize that the sin of this triangle is the sin of sin B... this means that both A and B are the same angle. The question is asking for the value of cos (A-B) and since A and B are the same the answer will be zero!
cos(A-B) = cos 0
= 1 < the answer is one because 1 is the raduis always 1 in the unit circle.
Question #4.

In this slide instead of having 2cos^2x+cosx-1=0 we let cosx=A so it's easier to read...
after we factored it to find the values of A.
- cosx = 1/2 is not a solution because it is in quadrants 1 and 4. So we move onto the next value which is x=π. This value works because it's greater than π/2 and smaller than 3π/2.

Okay, this is the last question of our pre-test. I was a bit confused when 1+cos2x changed to 1+2cos^2x-1 but you need to remember the identities because cos2x=2cos^2x-1. You also need to remember that sec^2x-1=tan^2.
When you repeatedly do the questions it's easier to remember all the identities...
* sorry if i didn't use colour or anything extra, i was using an older computer, at the time, and i was limited on tools. (: if i didn't anything wrong please comment & i'll correct it. The next scribe for wednesday is Bryan..
Monday, October 29, 2007
Sunday, October 28, 2007
Friday, October 26, 2007
Thursday, October 25, 2007
Identities
Well todays class, in my opinion went very quick yet it was compact because we were introduced a new topic in math today called Proofs of the Sum and Difference Identities.
First we started off the class with the usual identities problems. Nothing new there because it was all straight forward unless if you havent been doing your homework.
OK now onto math!

I know its a crappy picture but you can see it in todays slides none the less you should be able to recognize it.
1. Given sinA= 4/5 cosB=-5/13. With cosA<0>0. Find cos(A + B)
-The best start off for this question is to draw a diagram which we have done, just so it makes it easier to determine the equation that we will be using later on.
-Now, since we are trying to find cos(A + B) we will write the rest of the equation that goes along with it.
Recall:

Its the sine dance! The equation that goes along with cos(A +B) is written as: cos(A + B)= cosAcosB - sinAsinB
-Then we plug in the specified #'s from the diagrams we drew. So cosA is (-3/5) because in the alpha diagram the cosA is adjacent over hypotenuse. just keep plugging in the numbers for the rest of the equation.
-Once your done writing out the rest of the equation work them out by getting the common denominator. You should end up with the answer -33/65. Which results with the answer being in Quad. III.
Now its nearing the end of class and he quickly introduced Proofs of the Sum and Difference Identities.
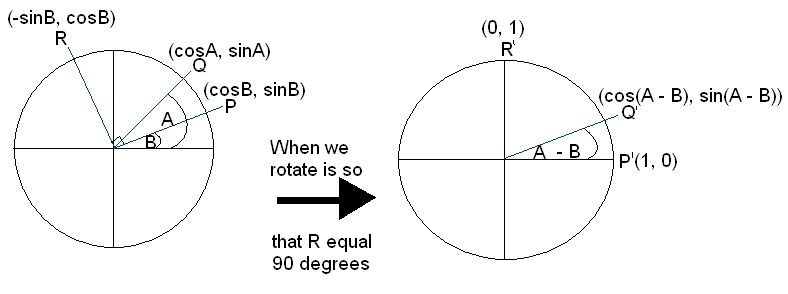
If we rotate diagram 1 so that R equals 90 degress and P is on the axis it will look like diagram 2. pretty much everything shifts clockwise.
Q'P' = QP
Now what we have to do is find the distance from Q'P' by using the distance formula:
= √((cos A- B) - 1)² + ((sin A - B) - 0)²
= √(cosA - cosB)² + (sinA - sinB)²
Around here Mr.K was totally rushing everything haha. Trying to finish the question before the bell rang. I didn't really understand a word he said after this plus I could no longer see the smart board cuz he was so busy writing.
Besides the end of the class it was pretty ok math that we learned today. Very understandable. Hope you got something out of my blog.
Drum roll please. "Attention! The next scribe is..........Derek!" ( I picked it randomly!)
Wednesday, October 24, 2007
Scribe Post, Monday Oct. 22 (Late) Alvin G.

Scribe Post: Trigometric Identities & the Sine Dance!
You can ask me tomorrow for the answer... agian."What is it that you cannot hold even ten minutes, even though it is lighter
than a feather."
I actually downloaded the SmartBoard Software and made a slide ^___^ but it turned out to be pretty small. It's better if you put it in full view.
I didn't explain all of the problems discussed in class because I don't believe that I have too. The best way of understanding this unit, I think, is by actually doing it. So have fun and DO YOUR HOMEWORK! (Which I believe is Exercise 14)
So sorry that I always post late!
Horray finally done! Now I don't have to worry for at least 2 months? Hopefully..
Next scribe is dun dun dunnnnnn
ALANANANABANANANANANANA
Tuesday, October 23, 2007
Scribe Post: Trigometric Identities
Anyways, I wanted to start off with the riddle I gave everyone.
“When you have it, you want to share it. Once you share it, you don't have it.”
No cheating! Let's see if you can get it and ask me tomorrow.
Okay moving on to math...
Today Mr. K gave us a surprise quiz. Well, I thought it was a surprise! I didn't expect it at all! I'm sure no one expected it too.
I’m not really articulate or good at explaining with words. It’s easier for me to describe something with pictures so I’m sorry if I don’t help make things clear but I’ll try my best!
Remember Mathematics is the science of patterns!It’d be easier if you could remember all the different things that equal to each other for this unit.
I’m really not good at this. I have no idea if there’s a simpler way of explaining this than what’s on the slide already. Hmm…
 So the first thing we have to do is change sec Θ and tan Θ to sine and cosine which becomes
So the first thing we have to do is change sec Θ and tan Θ to sine and cosine which becomes
Thus proving a) as the correct answer.

1st we have to change cos² Θ to sine. Because

Then you can manipulate it 1 - sec² Θ = - tan² Θ
Tah daH!
The Q.E.D. is an abbreviation of the Latin phrase "quod erat demonstrandum" (literally, "which was to be demonstrated", and figuratively, "I rest my case").
- Wikipedia
It’s basically saying that you have proven that it’s equal. In other words like saying, “HA! MY ANSWERS RIGHT!”
I feel like this scribe post was useless and ugly T_T …
Well, next scribe is ME! X)
Monday, October 22, 2007
Friday, October 19, 2007
Scribe Post: Trigonometric Idenities
now remembering back to yesterday Oct 18, we had two classes.
The First class we did a "pre-test" to prepare us for today's test hope everyone did well.
so now on with the new stuff well sort of...
Trigonometric Idenities:
In this unit the two important functions are sin(x) and cos(x) as we most of us may know already or will find out
using fundamental identities we can Simplfy a question

sin(x)sec(x)cot(x)
we know from the above image that sec(x) and cot(x) become 1/cos(x) and cos/sin(x)
now there will be a sin(x)cos(x) on both top and bottom of the fraction which will cancel out each other leaving 1.

and basicly thats about what we learned, as for next time i will try to be a little more careful and get this done much sooner sorry for the late scribe once again
looking at the list there some names that haven't been crossed out yet soooo next scribe is Alvin?
BOB
Thursday, October 18, 2007
B.O.B
BOB
-Alvin G.
B.O.B.
This is my second time taking pre cal 40s and i don't regret a thing. i didn't take two of the same courses with the same teacher nor at the same school. last year i took pre cal 40s at maples collegiate and i thought it was quite easy only if you did your homework every day. but once i returned back to Daniel McIntyre, i knew it would be challenging taking the course with Mr k. since i did once had him for my pre cal 20s. it's very different though i must say. the things we've just learned such as the word problems, I've actually never learned that, or maybe none that i know of and its very confusing but I've looked through the scribes and notes etc, and I'm quite sure i understand most of it. anyways, you'll hear more from me on the day before the next test.
Mr. K's pre cal 40s fall'07 class is a bunch of smart intelligent rabbits and i believe that every single one of my class mates will do terrific. just click on your heels three times and BAM!@#*! you'll do great! break a leg
B.O.B.
Cheers,
Ivanna
BOB
I also have trouble to graph for words problems. The hardest thing for word problem was how to get the period. I guess I understood how to get the period after Mr. K explained today's test.
I went over some of the examples, hoping that I do remember and do good on the test.
Good luck to everyone tomorrow! :)
BOB
This is rosselle by the way.. I used Jordan's account because i forgot mine...
Blogging On Blogging
One of my biggest mistakes and would cause me to lose a lot of marks is i don't fully understand or read a questions properly, mostly because i feel rushed to finish things within a time limit. So i will try to focus more on what the question is saying and write down important information before continuing on.
I believe i covered everything, now all i have to accomplish is to study more and use my spare time more efficiently
BOB 'in
The things i find most difficult about transformations is remembering the difference between f inverse and reciprocal. Also i have trouble remembering how to solve each of the transformations. In example today's pre test. when we were asked to write an equation for the inverse if the original equation. I understood that all the Y's be came X's and vice versa, except i forgot the steps on how to do it. I am also worried about the amount of stress tests put on me mentally. I just find it so nerve racking and i over analyse questions. I tend to panic. Some smaller things i have problems with is inverse. Such as labeling a scale.
Good luck to everyone tomorrow. I better go study
I got it mixed it up with eachother sometimes. But now since we went over it numerous times in class I finally got it. The other thing that also bothered me in this unit, was how to get the period of the function for the graph and how to find the equation. It got easier when we had to do those work sheets then go over it in class within the groups we were put in. Overall, I think this unit was alright. I'm just hoping I do good on the test tomorrow =/
-roslyn
BOB
Blogging on blogging
BOB
BOB
Blogging on Blogging
BOB
B.O.B.
Well first of all I can say that this is one part of the lectures that I am having trouble with. But as time goes on I understand little by little all the topics. Even though I am having trouble with some questions. At first I don’t understand if there is a number before the “x” for example: (1/2)x the graph will going to stretched even though it is a small number and the graph will going compress if the variable before the “x” is big for example: 2x.
Well at least now I know. And also at first I am having about the inverse function but because of our pre-test this early morning I barely understand now what is inverse function. Well I guess we really have to study hard to pass our exam tomorrow.
Good luck to us!!!!
BOB
Blogging on Blogging for Transformations
BOB
The other day, when we had our short quiz about graphing reciprocals I was kinda lost, and wasn't paying attention to the directions and cost me to loose marks. But after we corrected it I totally understand it now...i found out that this unit was way easier than the last unit.
Anyways, Goodluck to everyone!
BOB
GOOD LUCK EVERYBODY!!! ;P
Bob
Okay, now to start with Bob.
I've been able to understand everything we've done so far like the word problems and the transitions, except for graphing reciprocals. I understand where to put the asymtotes, I just don't know where to put the points and everything else from there.
I also have a problem paying attention to detail. I always make small mistakes on tests and quizzes that cost me to loose a lot of marks. It's just something I have to work on.
ganbatte minasan!
(Good luck everyone!)
- L i O N
BOB
I think I understand most of the part in this unit, Transformations.
The only thing that irritates me is when we are writing quizzes and tests,
I always make silly mistakes that i need to avoid. For example, I don't
read the questions carefully.
The grouping in class is fun. It makes us know other people in the class,
and learn the lesson better.
Aim to Ace the test! :D
Good luck to everyone!
Wednesday, October 17, 2007
Bob-ing
Well I guess I'll begin with my muddiest point(s). I really don’t like word problems. Period. It just throws me off somehow. I know how to do most of the work in this unit, just throw in some more words in the question and I suddenly don’t know what to do. Well that’s not the only thing that bothered me.
The type of word problem we did repeatedly in class with essentially the same questions gave me some constant trouble. Particularly where it asks “For how long…” or “At what time…” You know, the ones where it gives us the Y cord and we need to find the X cord(s). Yeah I don’t know how to completely.
Next I will explain that “moment of clarity” for me. It came with Reciprocal graphs. While I was doing my scribe for it I got some help and “poof”. It was explained to me as to how it worked. After I figured out how they worked I was really happy, because I could finish my scribe post!
On a side note…
Completely forgot how to do the calendar graphs until I seen it today on the review. Particularly the scaling. I know there’s some number system we did for the scale, and we were suppose to start at December something the year before. I don’t know…
Completely forgot about inverse functions until yesterday. Don’t know anything about them much…Switch the x and y cords? Isn't that the reflection in the y=x line? So is an inverse function just that? I don't know...
Having trouble remembering the different Stretches and what not.
One last questoin: How do you do a stretch on a line?
Aside from all that stuff above I think that I'm doing well with the other concepts.
Scribe Post
This present day we got straight to the point, and we began our second quiz on Transformations! woo.
20 minutes go by...
Sweat dripping on papers, palm's moist, and mouth's dry from the intensifying surge of power radiating from our quiz sheets. "Time's up! Time's up! Time's up!" yells Mr. Kuropatwa. Thirty sweat, and acne filled faces look up at the clapping hands of Mr. K as he commands us to advance our papers to the front of the classroom.
And so the alteration of our papers begin:

Odd Function: Symmetric with respect to the origin
Average-Minded Definition of an Odd Function: If you rotate the graph of the function 180 degrees: it'll be the same
We are told that this function is an Odd Function, ergo we must complete it.

This is the completed graph. woo.
Now let's put it to the test!...

Would you look at that! I have rotated the graph 180 degrees, and it looks completely identical!
Next question...

Graph the Reciprocal of the function.
Facts we know:
- Vertical Asymptote is where y= 0 because the reciprocal of the point is undefined
- The In-variant (unchanging) points are where y= 1, and where y= -1
- Class is long

Dotted Blue Line: Vertical asymptote, where y= 0
Yellow Points: In-variant points, where y= 1, and y= -1
Green Line: Reciprocal of the horizontal line coordinates (x= 2 - 4 , y= 3)
Next Question...
Next we are asked to sketch the graph of f(x) = 1 /| x-2|
To answer this question, we must first find the graph of f(x) = |x+2|
BUT BEFORE we find the graph of f(x) = |x+2|, we MUST first find the graph of
f(x) = x-2

Red Dot: -2 is a y-coordinate of the line
Blue Dot: Slope of the line is (rise/run) in this case it's (1/1); moving up once from -2, and moving to the right once ending in coordinates (x= 1 , y = -1)
To turn it into |x-2| : all negative coordinates turn positive:

To find the reciprocal of the function we use the
Facts We Know:
- Vertical Asymptote is where y= 0 because the reciprocal of the point is undefined
- The In-variant (unchanging) points are where y= 1, and where y= -1
- And yes class is long

Final Question...
With the function y= x , we are to expand it vertically by a factor of 2, shift it 3 units to the left, and take its reciprocal. With this new function we are asked to write a new equation for it, and sketch it on a graph.
First we'll write the Equation:
y = x
The first thing the question asks us to do is to expand the function vertically by a factor of 2. We accomplish that by writing
f(x) = 2x
Afterwards we must shift the function 3 units to the left, so the equation becomes:
f(x) = 2(x+3)
Finally we take it's reciprocal which is basically flipping it, switching the numerator, and the denominator's positions.
f(x) = 1/[2(x+3)]
or
f(x) = 1/(2x+6)
With this new equation; we can sketch the graph to this new function derived from y = x.
To sketch this function we must first sketch f(x) = 2x+6
6 - y-coordinate of function
2/1 - slope of function

Now we take the reciprocal of the function with our FACTS
- Vertical Asymptote is where y= 0 because the reciprocal of the point is undefined
- The In-variant (unchanging) points are where y= 1, and where y= -1

And there you have it a sketch of the new function.
-----------------------------------------------------------
It's been fun, I love spending my Wednesday mornings (2am) working on math stuff. Anyways here's a joke I have been holding in every time Mr.K asks us if we had any good jokes.
woo! Here it is:
An anion was walking down the street, and he saw a cation. The cation was looking pretty sad, so the anion went up to him, and asked him if anything was wrong. The cation looked at him and told him he had lost an electron. The anion asked him, "Are you sure?" and the cation said, "I'm positive!"
*Thanks Jasmin for refreshing that for me*
Hopefully you all understood that, I'm hoping.
SO, onto the juicy part that everyone skips to, and misses everything i wrote to check if they're the scribe post for the next day... muahaha time to put a frown on someone's face.
My buddy!! JOE S!! Your next, put down your psp.






















