Inverse functions can be solved in more than one way. Like the block of wood that Mr. K has, you can look at each of it's different sides but it's all the same block. The same goes with a function. You can figure out the inverse of a function by solving it numerically, algebraically, or graphically, and you'll end up with the same answer for all of them.
The whole idea of inverting a function is simple. All you really need is an input and an output. When the function is inverted the input and output switch. OR the output undoes what the input did. Mr. K told us a story as an example of how this inversion works. The original function would be Baby Play. clean room would be the input and the messy room would be the output. But once the parent cleans up the room, the room goes from a messy room to a clean room. This is the inverted function. Notice how they switched? Here's a diagram from the slide for better explanation.
Numerically
To figure out the inverse of an ordered pair ( x , y ) what happens is that the domain becomes the range, and the range because the domain. Domain being x and Range being y.

In this slide we solved the equations' inverse, algebraically. The y and the x switched. But an equation must be written as y = _____ . So we isolated the y. This same equation can be solved by using the table of values, but when doing so, you must undo the last thing you did to get the inverse.
*note: some functions cannot be solved with the table of values.
Graphically
When sketching a function on a graph, it's inverse can be found by switching obvious points. On the graph below, for example, It's points are (-6,-3) , (1,5) , (9,6). To find the inverse, the x's become the y's. y's become the x's.

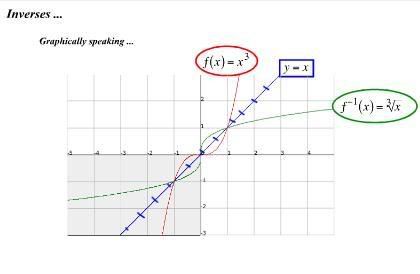
The function also flipped over the line y = x . Any points that lay on this line will not change because even when those points are inverted, it'll still be the same.
NEXT SCRIBE IS PAULO



No comments:
Post a Comment